2022. 7. 16. 21:35ㆍ공부/경영학도의 경제공부
mixed strategy (혼합 전략)에 대해서는 저번 포스팅에서도 다루었고 식도 썼지만
나를 정말 헷갈리게 했던 혼합 전략 계산법에 대해 다시 한번 훨씬 더 쉬운 버전으로 포스팅을 써본다
알고 나면 익숙해지고 쉬워지는 기초적인 것이지만
처음에 방정식을 세울 때는 저게 도대체 왜 저렇게 되는지 몰랐다..
그래서 블로그에 또! 메모 해두기로 😂
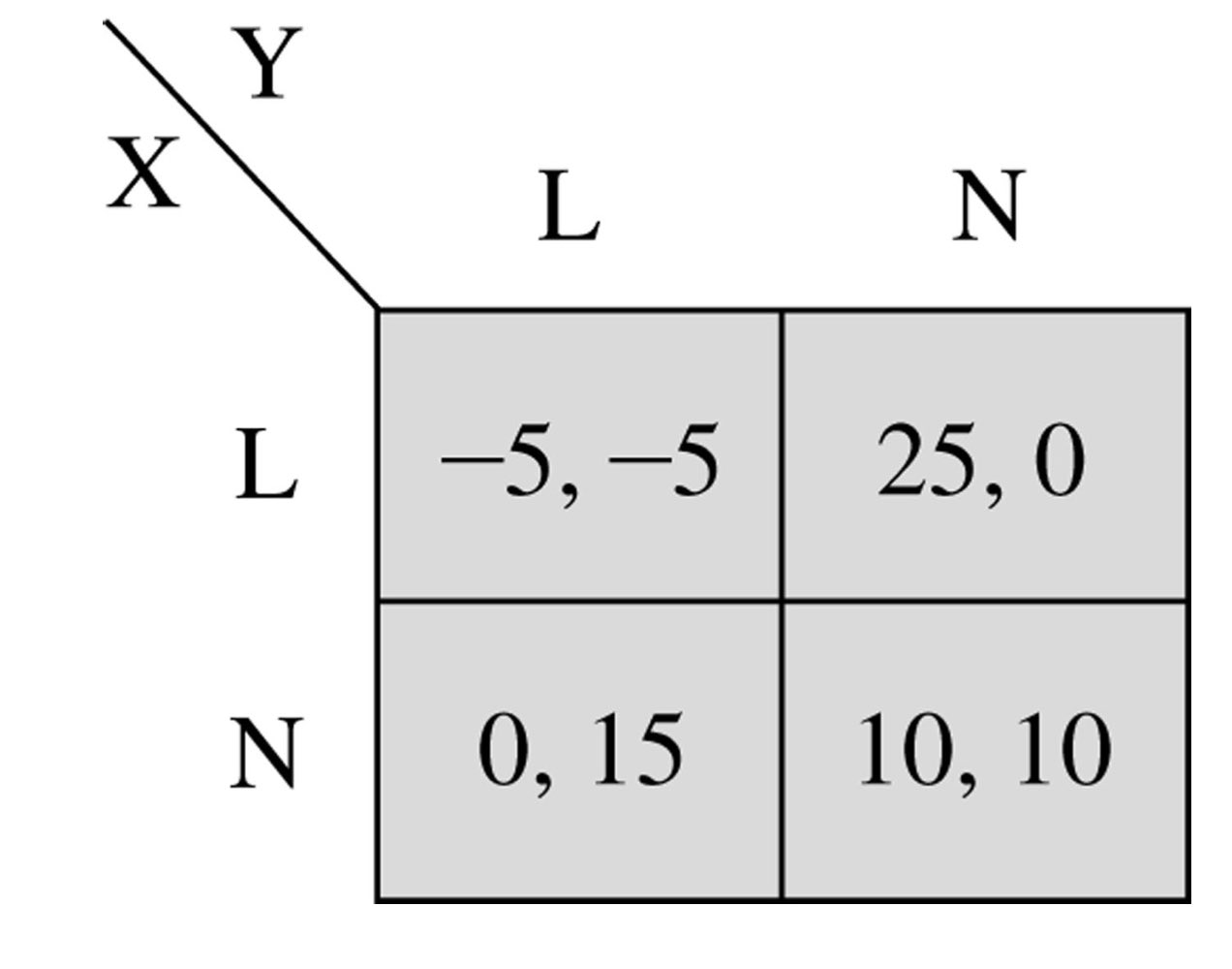
해당 게임에서 Mixed Strategy의 Nash Equilibria(내쉬 균형)을 구해보자
먼저 X가 L을 택할 확률이 p라고 하면 N을 택할 확률은 1-p이다.
마찬가지로 player Y가 L을 택할 확률을 q, N을 택할 확률 1-q하고 하면
방정식을 세울 때 P1의 기준에서 계산한다면 p(p1의 확률) x p2의 payoff를 하면 된다.
따라서
-5*p + 15*(1-p) = 0*p + 10*(1-p)
그러므로 이때 p의 값은 1/2이다.
마찬가지로
-5*q+25*(1-q) = 0*q + 10*(1-q)
q = 3/4
NE = {(1/2, 3/4)}
mixed strategy NE ->
- only rationalizable strategies are played with positive probability in mixed strategy equilibrium.
- all players are indifferent between all pure strategies used with positive probability.
내쉬 균형은 pure strategy(순수전략)의 경우 없을 수 있지만
mixed strategy에서는 항상 존재한다.
=> Every finite game has at least one Nash equilibrium in pure or mixed strategies. (Theorem (Nash, 1950))
'공부 > 경영학도의 경제공부' 카테고리의 다른 글
| Representativeness Heuristic(대표성 휴리스틱) (0) | 2022.12.19 |
|---|---|
| 유한반복게임과 무한반복게임 (Prisoners' Dilemma 죄수의 딜레마) (0) | 2022.07.20 |
| 경기자가 다수인 게임 e.g. 버스 하차 버튼 누르기 게임(calling an ambulance) (0) | 2022.07.13 |
| Nash Equilibrium과 Best Responce의 관계 (0) | 2022.07.11 |
| Best Responses - Example game (0) | 2022.07.08 |